Stress in the reinforcement s_s1 may be defined by calculation from bending moment M_Ed

or it can be set manually (when M_Ed = 0).

And _p‘ is area beforehand of afterwards stressed reinforcement in area A_c,eff

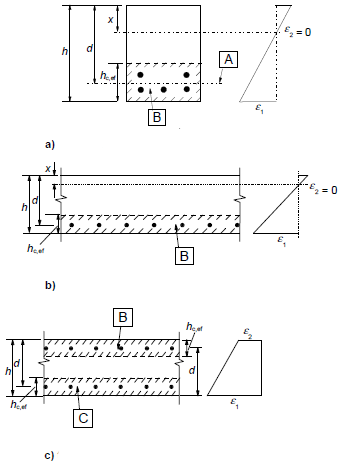
A_c,eff effective area of tension concrete surrounded by reinforcement of prestressed reinforcement in height h_c,ef  (see image 7.1)

h_c,ef is smaller from:

• 2,5(h - d)


• (h - x)/3


• h/2

Image 7.1 - Effective tension area (typical cases)

a) beam

b) plate

c) member in tension

[A] - center of gravity of reinforcement

[B] - effective tension area, Ac,eff

[C] - effective tension area near top suface, Acb,eff

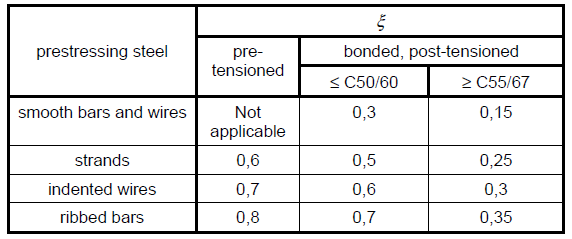
x  is ration of strength of prestressed reinforcement and reinforcement according to the table 6.2 in 6.8.2:

k₁ is coefficient of coherent parameters of reinforcement:

= 0,8 bars with big cohesion;

= 1,6 bars with smooth surface (e.g. presstresing bars);

k₂ is coefficient of ratio of deformation :

= 0,5 for bending;

= 1,0 for simple tension.

In cases of eccentric tension or local areas - the values k₂should be used, it is calculated by this formula:

k₂ = (e₁ + e₂)/2e₁

where e₁ is bigger ande₂ is smaller tension deformation ratio on edges of cross section, which is weakened by crack.

Values k3 and k4, which are used may be found in the nationa annex. The recommended values in Czech Republic (see NA 2.74):

k3 = 3,400

k4 = 0,425.

Table 7.1N - Recommended values w_max (mm)

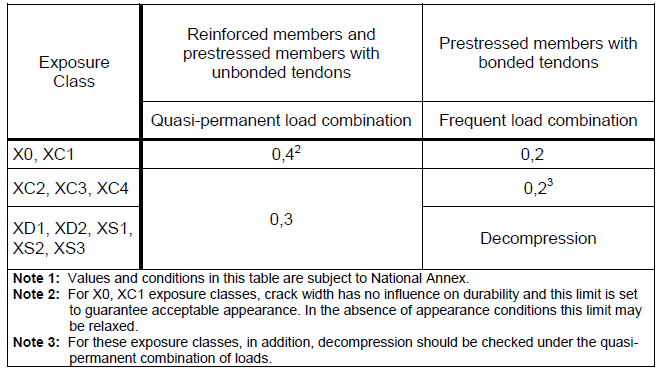
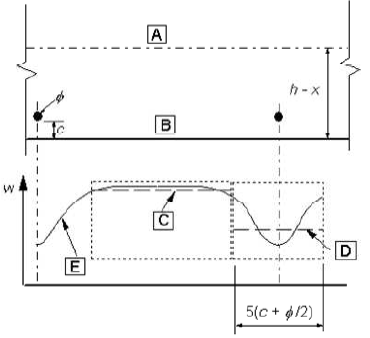
Image 7.2 - The crack on the concrete surface dependent on the distance from the bar

[A] - neutral axis

[B] - surface of tensioned concrete

[C] - expected crack width according to (7.14)

[D] - expected crack width according to (7.11)

[E] - real crack width